Your browser does not support the HTML5 canvas tag.

About this page

A triangle with the medians and centroids marked, and showing the region of all points which fall on multiple segments that divide the triangle in half.
The centroid (which falls on the three medians) is one point in this locus.

I created this page to explore a question I was curious about: What is the locus of points falling on multiple area-bisectors for a given triangle?

Details: Given △ABC, an area-bisector is a segment with endpoints on the triangle, which divides the triangle in half (by area). The triangle's three medians are examples of area-bisectors, and in fact, through every point on the boundary the triangle, there is exactly one such segment. However, for interior points, there are some points which fall on several area-bisectors—the most obvious of which is the centroid.

I determined that this locus is bounded by arcs from three hyperbolas. Full details are in given in the technical notes.

Out of curiosity, I expanded my exploration to quadrilaterals, which proved to be harder to describe. In particular, convex quadrilaterals have loci similar in shape to those of triangles (but somewhat distorted). For squares, rectangles, and parallelograms, the locus is a single point. For non-convex quadrilaterals, things get a lot more interesting, as evidenced by the pictures below; see technical notes for more information.

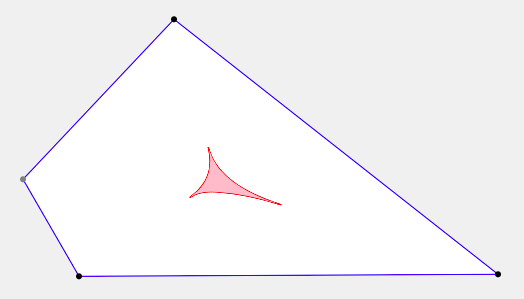
For a convex quadrilateral, the locus is still similar to that for a triangle.
For a convex quadrilateral, the locus is still similar to that for a triangle.
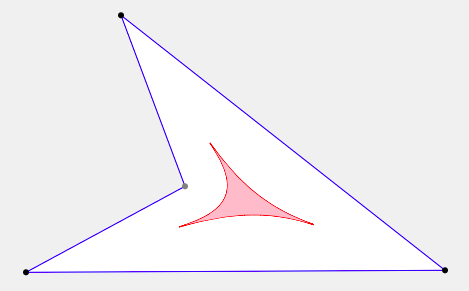
For non-convex quadrilaterals, the locus begins to become more complex.
For non-convex quadrilaterals, the locus begins to become more complex.
For a sufficiently non-convex quadrilateral, some of the area-bisectors cross outside the quadrilateral.
For a sufficiently non-convex quadrilateral, some of the area-bisectors cross outside the quadrilateral.

I have done little exploration with bowties (self-intersecting quadrilaterals), because they sometimes have boundary points which fall of no area-bisectors.

Not surprisingly, this is not the first exploration of the triangle bisector question. Here are links to two more:

Technical notes

For the triangle: Use a coordinate system with A=(-1,0), B=(1,0), and C=(a,b). Let A0, B0, and C0 be the midpoints of the medians of the triangle. The portion of the boundary between A0 and B0 is an arc of the hyperbola b^{2}x^{2}-2abxy-y^{2}\left(1-a^{2}\right)+2by-\frac{b^{2}}{2}=0. The other two boundary curves are equivalent hyperbolas (rescaled and rotated). Furthermore, this boundary consists of the midpoints of all of the area-bisector segments. Points on that boundary fall on exactly two area-bisectors, while points in the interior fall on three.

Because \text{area}(\triangle A_0B_0C_0)=\frac{1}{16}\text{area}(\triangle ABC)=\frac{b}{16}, and each of the hyperbolic arcs "carve out" \frac{3}{16}-\frac{\ln\left(2\right)}{4} of that area, that means that \frac{\text{locus area}}{\text{area}(\triangle ABC)}=\frac{3\ln\left(2\right)-2}{4}\doteq\ 0.01986.

Note: In my initial explorations, I thought that the arcs were three quadratic Bezier curves, with control points A0-M-B0, B0-M-C0, and C0-M-A0, with M the centroid of the triangle. Had that been true, the area of the locus would have been 1/48 the area of △ABC.

Release history

First official (beta) release: November 18, 2024.
Minor updates (including touch support for mobile use, still somewhat buggy): November 19, 2024.
Added (and corrected) some descriptive information: December 12, 2024.

The contents of this page are © 2024 Darryl Nester. It is available to anyone who wishes to use it (like most things on the Internet). Please send me an email if you have found it to be useful, or if you have suggestions.