Initial point: blah

lock t=0 on the left — zoom +  copy download   < pan >

Comments / notes: Click anywhere to edit Use these links to save/share models. (Comments/notes are NOT included in these links.) copy Short link (current tab) copy Long link (all tabs)

Plain-text(ish) summary of current model (all tabs) Note: This summary includes any comments. If you edit this summary (or paste in a new summary) and click "submit," the models are changed accordingly.

Users enter a first-order ODE in the form dy/dx = f(x,y), or a system in the form dx/dt = f(t,x,y) and dy/dt = g(t,x,y). (Note: A limited number of alternative variables can be chosen, to make it easier to adapt to different applications or textbook conventions.)

For ODEs, a slope field is displayed; for systems, a direction field is shown. (In the case of non-autonomous systems—that is, where either dx/dt or dy/dt depends on t—the direction field shown is for t = 0.)

By specifying initial values, users can see approximate solution curves, with several choices for the solution method (click links to read more at Wikipedia):

• Euler method
• Improved Euler (Heun's) method
• Midpoint method
• Runge-Kutta (both RK4 and the "3/8 rule")
• Runge-Kutta-Fehlberg (RKF) BETA - only working for ODEs [Sept 22 2020]

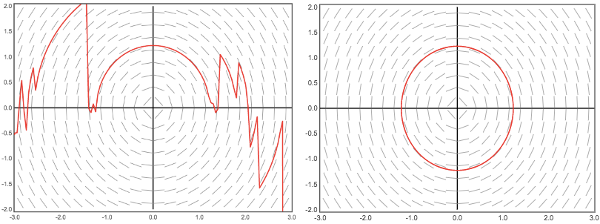
The "switching" option next to the choice of method is an adaptation that produces better solution plots in some cases. It affects all of the numerical methods for ODEs except for RKF (it has no effect on solutions for systems). Specifically: If, at any point, |dy/dx| > 3 (i.e., if the tangent lines get too steep), the method switches the roles of x and y. For example, for the DE dy/dx = -y/x (a circle), here are solution curves for RK4 with h=0.05 without switching (left) and with switching (right):

For the most part, expressions are entered using standard mathematical notation, with a few caveats:

• Multiplication is implied in expressions like:
  • 2x(3x^2-1)
  • cos(x)sin(x)
  • (x+1)(x-2)
  • ln(4)4^x
  • x|x+1|
  • x cos(x) or x y (There must be a space between x and cos, or x and y.)
• Closing parentheses are not optional (unlike, say, on TI-84 graphing calculators).
• All functions must have parentheses—for example, use sin(x) rather than sin x, and ln(|x|) rather than ln|x|.
• Exponentiation (like 7^x) can be entered as either 7^x or power(7,x), and e^x can be entered as e^x or exp(x). (Note that e^2x is e²x.)
• The inverse trig functions should be entered as atan, asin, and acos (and similarly for inverse hyperbolic trig). However, some alternate notations are also accepted (for example, arctan).
• Absolute values can be entered as either |x| or abs(x).
• For numerical input (such as the coordinates for an initial value), fractions and expressions are allowed; for example, you can enter 5/3 instead of 1.6666666667, or sqrt(2), or pi/2.
• e can be entered as a simple constant (as can pi), but take care, because e also is used in exponential notation. For example, I once solved an IVP for which the constant was C=2e+1, and realized that I got the correct plot when I entered …+(1+2e)e^(-x), while …+(2e+1)e^(-x) produced the wrong graph, because 2e+1 is interpreted 2×10¹=20.
• In addition to many standard functions (and some exotic ones), the following functions can be helpful for some DE modeling problems:
  • if(condition, true-value, false-value) or when(condition, true-value, false-value). This can be used to create piecewise-defined functions, such as when(x>0,x^2,y).
  • step(x,a) is the unit step function, equivalent to when(x>a,1,0). The value of a defaults to 0 if omitted.
  • delta(x,k) approximates the Dirac Delta function using the Gaussian function exp(-(x/k)²)/(|k|√π). The value of k defaults to 0.01 if omitted.

I created this page as a replacement for the very nice JODEapplet by Marek Rychlik. I had used his Java applet for many years in my Calculus 2 and DE classes, but began to have issues with unstable Java installations and nuisance security alerts. (In particular, I never know if a particular classroom's computer will be able to run it.) This page is written in JavaScript (not Java), so it does not have those compatibility and security issues. In addition, your Web browser's "zoom" features will work with this page (often not the case with Java), so you can increase the display size if you need to do a demonstration for a large class.

Thanks to many users for helpful feedback, especially to Larry Friesen at Butler Community College, who suggested many improvements to this page, and (with his colleagues and students) tested it extensively.

NOTE: If this page is misbehaving, it may be that your browser is still using an old version of one of the support files. You might be able to fix this by clearing your browser's cache (click THIS LINK to find instructions) and then reloading this page. If this does not work, please contact me and describe the problem you are having.

Condensed release history:

(November 4, 2022) A few alterations to the interface, but mostly correcting some bugs introduced in the previous update.

(November 2, 2022) In specifying DEs, or in graphing exact solutions (functions, parametrics, etc.), you can can include constants A,B,C,D,K,M,N,P,Q,R, and then vary the values of those constants to see the effect on the solution. For example, try:

• dy/dx=y^2 cos(x)
• this damped pendulum problem.
• A general linear system.

Note that this feature should still be considered "beta"; when it works, it's pretty cool, but things can go wrong (e.g., in some situations, a graph might not update when a value is changed).

(October 15, 2022) Corrected/improved some interface issues. Can graph (any number of) function/parametric/polar/implicit plots.

(September 22, 2020) Runge-Kutta-Fehlberg method (beta).

(August 28, 2020) Added ability to overlay up to four graphs of functions, plus minor interface tweaks.

(November 5, 2018) Fixed some glitches in the "preset" menu.

(February 11, 2018) Minor bug fixes, and added (beta) support for polar-coordinate ODEs and systems.

(October 2, 2017) Added descriptions of if/when, step, and delta functions. Overhauled to remove MooTools dependency.

(March 1, 2017) Added an explanation of the "switching" option (see "How to use this page").

(February 1, 2017) When a link includes initial-value points, the last of these points shows up in the input boxes.

(March 11, 2016) Recognizes when an initial value is an equilibrium point; zooming/panning and tracing (via hovering) on timeplots. Phase plane curves default to "t>0" only; this is controlled by the "lock t=0" option under the timeplot.

(February 25, 2016) Create time plots for systems, and allow limited changes to the names of the independent and dependent variables (e.g., x and y, or y and t, etc.)

(October 9, 2014) Added support for systems with two dependent variables. (October 16) Improved support for systems; they are now included in the link, and the solution tables are formatted better. (October 27) Some system presets included. You can also save the graph as a PNG file, or open it in a new window, using the given link, or by right-clicking on the link. You can also copy the image to the clipboard (though perhaps not on all systems). Note: In Firefox, "View image" will open the image IN THE CURRENT WINDOW.

(September 3, 2014) First release. Tested on Chrome (fairly extensively), Firefox (less), and Explorer (minimally). Reasonably functional, but incomplete. (September 7) Added numerical tables and extended addresses (with updating link to current state of the page). (September 9) Added the option for selectable "presets." The "BDH" presets are exercises from Differential Equations, Blanchard/Devaney/Hall, 3rd edition (mostly). (September 11) Tweaked some features, and added a couple of additional methods.

TODO:

• Improve support for mobile devices, iPads, etc.
• Display the initial point for each curve.
• For non-autonomous systems, allow user to select the value of t for which the direction field is displayed.
• Improve behavior/options for RKF, and possibly add other adaptive methods.

---

The contents of this page are © 2022 Darryl Nester. It is available to anyone who wishes to use it (like most things on the Internet). Please send me an email if you have found it to be useful, or if you have suggestions. (In particular, if you have a "preset" you would like to suggest, email me the link above.)