Secret Santa Server

For restrictions, a check (or X) means that combination is not allowed.
check for symmetric restrictions (that is, if A cannot pick B, then B cannot pick A).

check here to supply email addresses (which do not have to be unique) for some or all members of the exchange. Step 4 (notification) might be slightly easier if you enter email addresses. No email addresses are saved by this Web site, and all email messages will be sent by you, not by bluffton.edu.

You can save this information, along with the current set of matches, in one of two ways:

in a cookie (for this browser only)—if your browser is set to allow them.

when restrictions are complete (or to generate a new set of matches).

This can be done in two ways:

	plain text—which means that anyone can read it (including you).	Message for:
	secret code—which can be deciphered by visiting the decoding page. This option might be preferred if some members of the exchange share the same email address—although obviously, anyone who knows the secret code can visit the decoding page.
Using either method, you can do one or both of the following:
º	showing all matches. Each match will be on its own line, in plain text in code, along with the address of the decoding page. This page can then be printed, and either saved for reference, or cut into individual strips and distributed. Note that if your browser has a pop-up blocker, it might not allow this.
º	Send an email message to each person.
	Check here if you send/receive email using a separate program (such as Outlook, Apple Mail, or Thunderbird). The buttons on the right will then create a new message using that program. Leave the box unchecked if you use a Web-based mail account (such as Gmail, Yahoo! Mail, Windows Live Mail, or Outlook Web Access). You may then copy the message from the box into a new message to each person.

While I designed this page to make it easier for my family to choose names each Christmas, I have used it as the basis for talks at Bluffton University (as part of our Mathematics Seminar), and at Miami University (at the 2015 Mathematics Conference on "Combinatorics and its Applications"). I've included links to Wikipedia to supplement the minimal technical detail given below.

You can find a fair amount of information (including most of what follows) in the PDF file from my talk at Miami.

For a group of n people, a particular set of assignments (that is, who picked who?) is equivalent to a permutation of the numbers {0, 1, 2, …, n–1}. For example, with 4 people, {2,3,1,0} (henceforth 2310, without the commas and braces) means that person 0 chose person 2, person 1 choose person 3, etc. A "basic" gift exchange (with no restrictions except that a person may not choose his/her own name) is a special kind of permutation called a derangement. For a group of n people, the number of derangements is D_n = 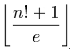floor of (n!+1)/e . I used the algorithm to generate random derangements published by Martínez, Panholzer, and Prodinger in the 2008 SIAM ANALCO Proceedings.

With additional restrictions, this number is obviously reduced. The number of possible selections given above is found using rook polynomials, which you can learn more about at my page on the subject, or other places on the Web such as Wikipedia.

Once a particular set of assignments is chosen (e.g. 2310 or 53740126), we index the permutation by assigning a number from 0 to n!–1 so that (e.g.) for n=4, 0 ↔ 0123, 1 ↔ 0132, …, 23 ↔ 3210, or for n=5, 0 ↔ 01234, 1 ↔ 01243, …, 119 ↔ 43210. The relationship between the index and the permutation is detailed in this PDF file (beginning on page 3).