Walsh Cyclopropane Molecular Orbitals
Rigorous Derivations
Rigorous derivation of the A1' cyclopropane MO from the A1 MOs of the methylene fragments.
There is one identical σ-type orbital on each of the three
carbon atoms. Let the orbital on C1 be φ1s, that on C2 be φ2s, and that on C3 be
φ3s.
We now apply the A1' projection operator
PA1' to one of the three orbitals, let us say
φ1s. In order to do this, we
apply each symmetry operation in turn, multiplying the result by the character of the
A1' representation.
| D3h | |
E |
2C3 |
3C2 |
σh |
2S3 |
3σv |
|
| A1' | |
1 |
1 |
1 |
1 |
1 |
1 |
| PA1'φ1s |
≈ |
φ1s +
φ2s + φ3s + φ1s + φ2s + φ3s + φ1s + φ2s + φ3s + φ2s + φ3s + φ1s |
| |
= |
4(φ1s +
φ2s + φ3s) |
|
≈ |
φ1s +
φ2s + φ3s |
| |
| The MO is therefore |
 |
|
| Normalized: |
| |
ψA1' |
= |
1 |
(φ1s + φ2s + φ3s) |
|
| √3 |
|
Return
Rigorous derivation of the σ-type E'
cyclopropane MOs from the A1 MOs of the methylene
fragments.
There is one identical σ-type orbital on each of the three
carbon atoms. Let the orbital on C1 be φ1s, that on C2 be φ2s, and that on C3 be
φ3s.
We now apply the E' projection operator PE' to one of the three orbitals, let us say φ1s. In order to do this, we apply
each symmetry operation in turn, multiplying the result by the character of the
E' representation.
| D3h | |
E |
2C3 |
3C2 |
σh |
2S3 |
3σv |
|
| E' | |
2 |
-1 |
0 |
2 |
-1 |
0 |
| PE'φ1s |
≈ |
2φ1s -
φ2s - φ3s + 2φ1s - φ2s - φ3s |
| |
= |
2(2φ1s -
φ2s - φ3s) |
|
≈ |
2φ1s -
φ2s - φ3s |
| |
| The MO is therefore |
 |
|
| Normalized: |
| |
ψE',a |
= |
1 |
(2φ1s - φ2s - φ3s) |
|
| √6 |
|
But we need another orbital. In order to do this, we need to pick a symmetry operation
belonging to the D3h group which will convert ψE',a into something other
than ±1 times itself. For example, C3:
The new function is not orthogonal to ψE',a, and so it must be a linear combination of ψE',a with some other
function, ψE',b. To
find ψE',b we multiply
the new function by some appropriate factor, then subtract ψE',a from it:
| |
2(2φ2s -
φ3s - φ1s) + (2φ1s - φ2s - φ3s) |
| = |
4φ2s -
2φ3s - 2φ1s + 2φ1s - φ2s - φ3s |
| = |
3φ2s -
3φ3s ≈ φ2s
- φ3s |
| |
| The MO is
therefore |
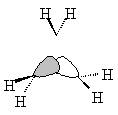 |
|
| Normalized: |
|
Return
Rigorous derivation of the A2' cyclopropane MO from the B2 MOs of the methylene fragments.
There is one identical π-type orbital on each of the three
carbon atoms. Let the orbital on C1 be φ1p, that on C2 be φ2p, and that on C3 be
φ3p.
We now apply the A2' projection operator
PA2' to one of the three orbitals, let us say
φ1p. In order to do this, we
apply each symmetry operation in turn, multiplying the result by the character of the
A2' representation.
| D3h | |
E |
2C3 |
3C2 |
σh |
2S3 |
3σv |
|
| A2' | |
1 |
1 |
-1 |
1 |
1 |
-1 |
| PA2'φ1p |
≈ |
φ1p +
φ2p + φ3p - (-φ1p - φ2p - φ3p) + φ1p + φ2p + φ3p - (-φ1p - φ2p - φ3p) |
| |
= |
4(φ1p +
φ2p + φ3p) |
|
≈ |
φ1p +
φ2p + φ3p |
| |
| The MO is therefore |
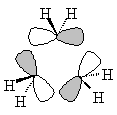 |
|
| Normalized: |
| |
ψA2' |
= |
1 |
(φ1p + φ2p + φ3p) |
|
| √3 |
|
Return
Rigorous derivation of the π-type E'
cyclopropane MOs from the B2 MOs of the methylene
fragments.
There is one identical π-type orbital on each of the three
carbon atoms. Let the orbital on C1 be φ1p, that on C2 be φ2p, and that on C3 be
φ3p.
We now apply the E' projection operator PE' to one of the three orbitals, let us say φ1p. In order to do this, we apply
each symmetry operation in turn, multiplying the result by the character of the
E' representation.
| D3h | |
E |
2C3 |
3C2 |
σh |
2S3 |
3σv |
|
| E' | |
2 |
-1 |
0 |
2 |
-1 |
0 |
| PE'φ1p |
≈ |
2φ1p -
φ2p - φ3p + 2φ1p - φ2p - φ3p |
| |
= |
2(2φ1p -
φ2p - φ3p) |
|
≈ |
2φ1p -
φ2p - φ3p |
| |
| The MO is therefore |
 |
|
| Normalized: |
| |
ψE',c |
= |
1 |
(2φ1p - φ2p - φ3p) |
|
| √6 |
|
But we need another orbital. In order to do this, we need to pick a symmetry operation
belonging to the D3h group which will convert ψE',c into something other
than ±1 times itself. For example, C3:
The new function is not orthogonal to ψE',c, and so it must be a linear combination of ψE',c with some other
function, ψE',d. To
find ψE',d we multiply
the new function by some appropriate factor, then subtract ψE',c from it:
| |
2(2φ2p -
φ3p - φ1p) + (2φ1p - φ2p - φ3p) |
| = |
4φ2p -
2φ3p - 2φ1p + 2φ1p - φ2p - φ3p |
| = |
3φ2p -
3φ3p ≈ φ2p
- φ3p |
| |
| The MO is therefore |
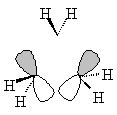 |
|
| Normalized: |
|
Return
Copyright © 1997 by Daniel J. Berger. This work may be copied without limit if
its use is to be for non-profit educational purposes. Such copies may be by
any method, present or future. The author requests only that this statement
accompany all such copies. All rights to publication for profit are retained
by the author.
Images generated with HyperChem Lite and ChemWindow Suite.