|
|
NSC111: Physics/Earth/Space
|
RelativityFair warning: most of what we will discuss is counter-intuitive. The reason is that our intuition is shaped by our experience--and we have no experience with either high velocities or strong gravitational fields. The Principle of Relativity: all observers see the same laws of nature.There are three types of relativity:
For the ancients, spacetime is modeled very much as our diagram. There is absolute space and absolute time, and one can always define one's position in either space or time without reference to some other worldline. The result is that all observers can agree on where and when an event occurs. But Galileo realized that this need not be so. If we stand on the deck of a moving ship, the world is rushing by and a mast, for instance, is fixed in a single position. But to an observer outside the ship (say, a whale watching the ship go by) the mast moves with the ship, and where the mast is changes from moment to moment. And for an alien observer in a UFO... ship, mast and whale are all in motion at about the same speed and do not occupy any fixed position! Observers need not agree on where something happens. Absolute space can only exist if one observer is always defined as being "at rest." But any frame of reference can validly consider itself "at rest!" I diagrammed the ship, whale, and alien worldlines in class. Nevertheless, it is simple to transform the shipboard frame of reference into the whale's frame of reference. Even if the ship is in non-uniform motion, as long as we have a complete accounting of the velocity of the ship over time we can account for every position that the whale sees the mast to occupy. While we may arbitrarily define one worldline as being vertical (that is, not moving in space), all observers can agree on when something happens. A discussion in terms of a train was given in class. Suppose you are standing by the tracks, and a train is going by. Suppose someone is bouncing a superball between the floor and ceiling of the train. To the person in the train, the superball will be moving with some up-and-down velocity v1, and it moves through a distance equal to v1t. This is shown below. 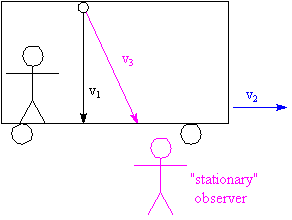 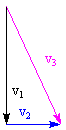 The train itself is moving with some other velocity v2, and moves through a distance v2t. A stationary observer sees the ball moving some greater distance, a composite of the distance the ball moves within the train and the distance the train itself moves, which we can represent as v3t. The speed the stationary observer sees the ball moving is v3.
The train itself is moving with some other velocity v2, and moves through a distance v2t. A stationary observer sees the ball moving some greater distance, a composite of the distance the ball moves within the train and the distance the train itself moves, which we can represent as v3t. The speed the stationary observer sees the ball moving is v3.
From the Pythagorean theorem, we can calculate the value of v3 according to the diagram at right. The velocity seen by the stationary observer is given by But it became clear in the 19th Century that, in order to have absolute time, you have to have absolute space--some frame of reference must be truly stationary. In 1887, Michelson and Morley tested this idea (I am analyzing the Michelson-Morley experiment in hindsight; they didn't think any such thing! They were looking for increases and decreases in the speed of light caused by the Earth's motion!) and found that it didn't work. The speed of light is constant. From a different perspective, Maxwell had already shown that the speed of light is not arbitrary, but a consequence of the laws governing electricity and magnetism. So if the Principle of Relativity is correct and all observers do see the same natural laws, we are led to Einstein's Second Postulate: The speed of light is the same in every inertial frame of reference.What this can mean for the concept of "absolute time" can be shown by our train analogy. Suppose, instead of a ball, we have a beam of light bouncing between mirrors on the floor and ceiling of the train. But the second postulate of Special Relativity guarantees that both the observer in the train and the "stationary" observer see the same speed of light! So if the light travels a greater distance for the "stationary" observer (distance is always equal to vt), yet at the same speed c, the thing that must be different is the time the stationary observer sees!
But time is even more variable than this: two observers, traveling at different speeds, cannot even agree on when something happens because they get their information from light beams, which travel at a finite speed. The following is taken from a more detailed discussion of Einstein-Minkowski Spacetime at The Light Cone.Suppose that Mary is riding a train, and happens to be standing exactly midway between the front and back of the train. Suppose further, that Susan is standing along the tracks on which Mary's train is moving. Just as Mary and Susan come even with each other, lightning bolts strike the front and back of the train. The lightning bolts each leave a mark on the train, and a mark on the tracks. The light from the two lightning bolts reaches Susan simultaneously, but because Mary is moving toward the first beam of light and away from the second, the "front" light reaches her before the "rear" light.
It should be easy for you to show that, for the lightning events to happen simultaneously for Mary (on the train), Susan would have to see lightning strike the rear of the train before it struck the front. General Relativity
Consequences are explained well in your textbook and in some of the links given below; they include the following:
For further information about relativity, see
|
|
Copyright © 2001 by Daniel J. Berger. This work may be copied without limit if its use is to be for non-profit educational purposes. Such copies may be by any method, present or future. The author requests only that this statement accompany all such copies. All rights to publication for profit are retained by the author. |